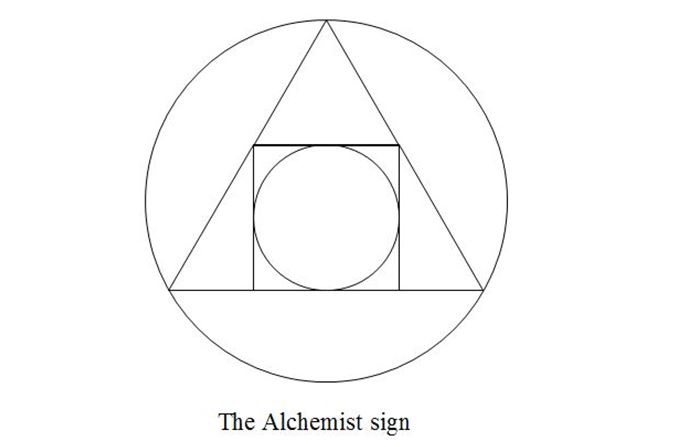
Visiting my home town of Leeds recently, my relatives took me to a restaurant in the city centre called The Alchemist. The sign above the door and on their business cards caught my interest.
All kinds of maths sprung to my mind.
Symmetry. Construction. Pythagoras. Trigonometry. Surds. Proof.
The symbol could be presented to students of almost any level of ability. The questions could range from something as open as ‘Do some maths with that’ to a more specific ‘What is the ratio of the circumferences of the two circles?’, or ‘Prove that the circles do not have the same centre’. Even a vocabulary test of ‘name the shapes that you see’ (or ‘identify the following’) would generate: circle, equilateral triangle, isosceles triangle, square, segment, chord and trapezium.
There are some dangerous misconceptions to iron out first – for example, the belief that the top corners of the square lie at the midpoints of the sides of the equilateral triangle. This could be disproved formally for higher ability students, or if a drawing of the symbol was given to the students a little exercise in transformations using tracing paper would show this to be false. The same method would work to prove the circle centres are not concurrent.
Construction
The complete symbol can actually be constructed using only basic constructions present in the GCSE syllabus. The key is to start with the square and work from there.
- Construct a square of given length by constructing a right angle at the end of a line segment. A 5 cm square in the centre of an A4 sheet of paper works nicely, in that the final shape will fit on the paper.
- Draw in the diagonals to find the centre for the smaller circle.
- Draw the circle.
- Construct an equilateral triangle on the top of the square.
- Extend the base of the square either side.
- Extend the small equilateral triangle until it reaches the extended base.
- Bisect the three sides of the large equilateral triangle.
- Join the midpoints to the opposite corners to construct the medians.
- They meet at the centre of the large circle. Draw the large circle.
I cannot see a way to construct the symbol starting with the outside circle. Is there a way?
Download my worked example of the construction of the Alchemist symbol.
Pythagoras’ Theorem
Rather than construction, the shapes could be drawn by working out the lengths using Pythagoras’ Theorem. Alternatively, a question could be set asking for the lengths of each component in relation to a starting measurement for the square, for example.
Trigonometry
Trigonometry could be used. With just 60° (or 30°) involved, the special values of sin60° and cos60° could be required, bringing into play some useful practice manipulating surds.
For both Pythagoras and trigonometry, discussion or use of similar shapes and scale factors could be employed. Together with surds, reciprocals can be brought in through use of equivalent ratios.
Symmetry
For those willing to expand students’ general knowledge, there are hundreds of alchemy symbols to consider mathematically. The sample below might provide a diversion from the more mundane shapes used for reflection and rotation symmetry. A word of warning however – alchemy can be connected with the occult, and searches on the internet may lead to places that are undesirable for students.
Thanks for reading,
Steve Fearnley
Steve Fearnley, MA MEd PGCE, has been a maths teacher for over 30 years as well as being a deputy headteacher. He is now a private maths tutor, covering KS3 up to A Level, as well as an author for both MyMaths.co.uk and our brand new AQA GCSE Maths Student Books.